
Jeg ved godt at jeg savner mit arbejde. Meget endda. Eleverne, kollegerne, selve det at undervise,… Min underbevidsthed ved det tydeligvis også, at dømme efter det hint den smider efter mig hver dag. Ovenfor ses afbilledet min daglige thetids-ostemad. Først i dag lagde jeg mærke til at det er en rigtig matematiklærermad. Kan du også se det?(Kig lige efter igen 😀) Ellers kommer forklaringen nedenfor…
Min ostemad viser et geometrisk bevis for regnereglen “Første kvadratsætning”, som lyder sådan her:
(a+b)2=a2+b2+2ab
I matematik er et bevis et stringent argument for at noget passer, altså i dette tilfælde en argumentation for at de to sider af formlen ovenfor faktisk er lig med hinanden. Lad os se hvordan det passer med ostemaden:
Kald sidelængden af det lille kvadrat for a og sidelængden af det mellemstore kvadrat for b. Så må hver side af ostemaden være a+b lang: (kig på billedet herunder, og overbevis dig selv om hvorfor det må være rigtigt før du læser videre.)
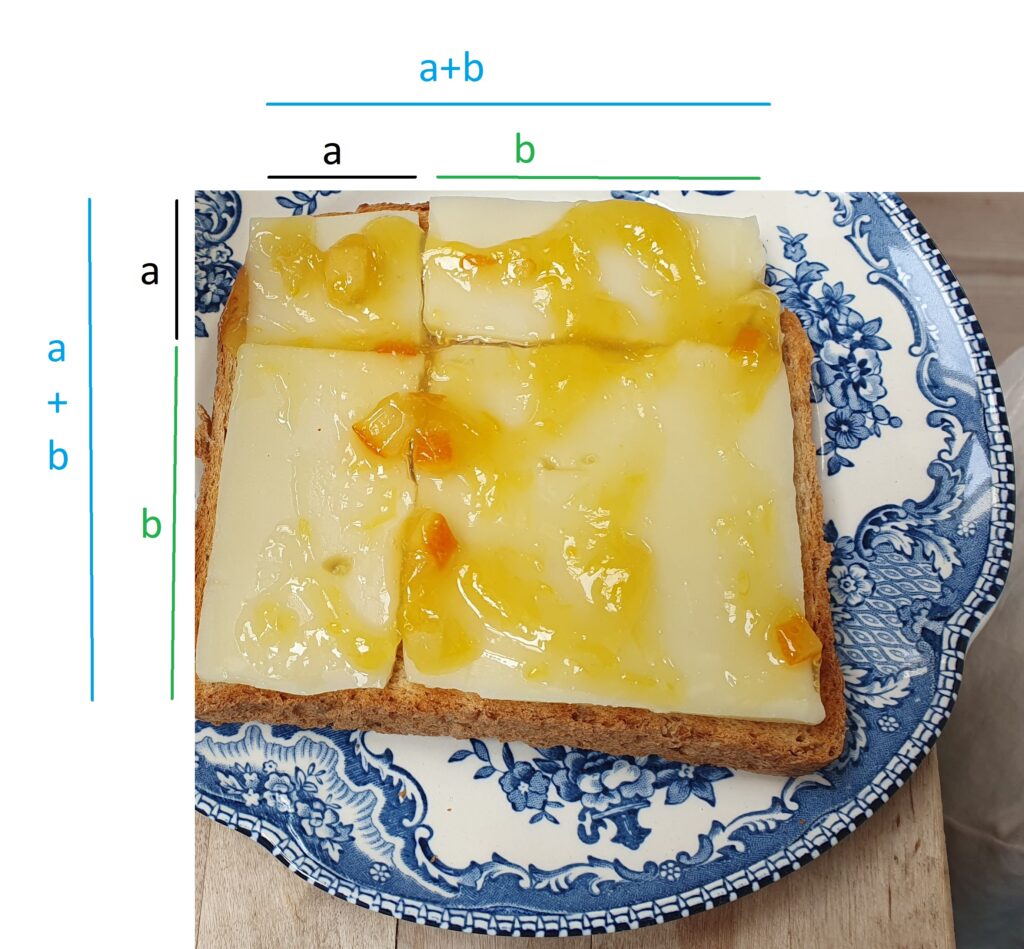
Lad os nu se på arealerne. Arealet af hele ostemaden må være de to sider ganget sammen, altså
areal af ostemad = (a+b)*(a+b)
Når noget er ganget med sig selv, så plejer man at skrive “i anden”, altså f.eks. 3*3=32 eller 27*27=272. Altså kan jeg skrive arealet af hele ostemaden som
areal af ostemad = (a+b)2
Bemærk at det er præcis venstre side af vores regneregel “Første kvadratsætning” som jeg gerne vil bevise er sand.
En anden måde at finde arealet af ostemaden er at finde arealet af delene af den hver for sig, og så lægge dem sammen til sidst. Hvis vi ser på billedet nedenfor, så kan vi se at arealet af det lille kvadrat er a*a=a2, at arealet af det lidt større kvadrat er b*b=b2. De to rektangler er ens, og deres areal er a*b. (Kig igen på billedet herunder, og overbevis dig selv om at det er korrekt).
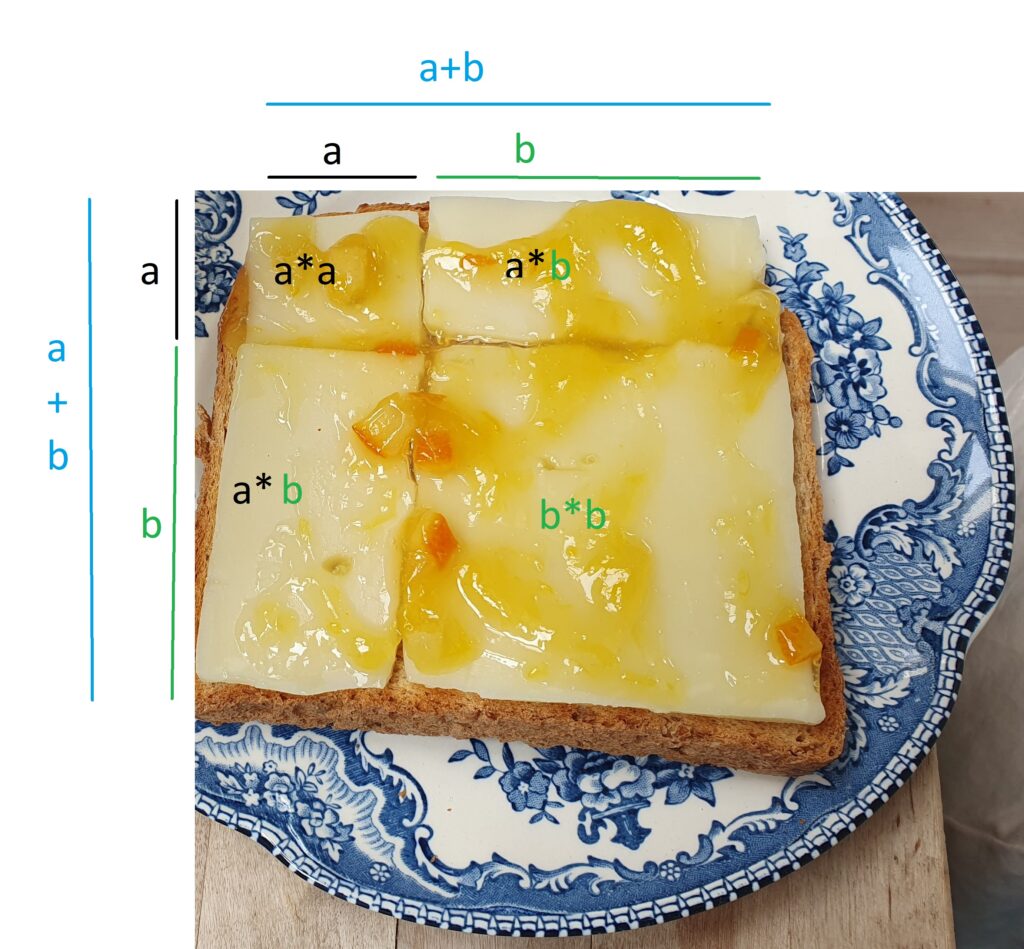
Lægger jeg de fire dele sammen så får jeg altså at
areal af ostemad = lille kvadrat + større kvadrat + 2rektangler = a2+b2+2a*b
Men ostemaden er jo lige stor, uanset om jeg beregner arealet på den første, eller på den anden måde. Så de to udtryk jeg er kommet frem til er lig hinanden. Altså får jeg, når jeg sætter de to udtryk ind, at:
areal af ostemad regnet som en hel mad = areal af de fire dele lagt sammen
(a+b)2= a2+b2+2ab
Og det er jo præcis den regneregel jeg gerne ville bevise 😎
Ahhhhhh 😊 Det føltes godt! Kunne du følge med hele vejen? Hvor faldt du eventuelt af? Fortæl mig om det i facebook-kommentarerne, for jeg er vældig nysgerrig 🤩
No comment so far